
Propočet úhlu a sklonu pyramid
=========
Jaké tajemství skrývá Cheopsova pyramida?
=========
Propočet poměrů sklonu strany, úhlu stěny a poměr plochy u Cheopsovy pyramidy tak, jak je ve skutečnosti:
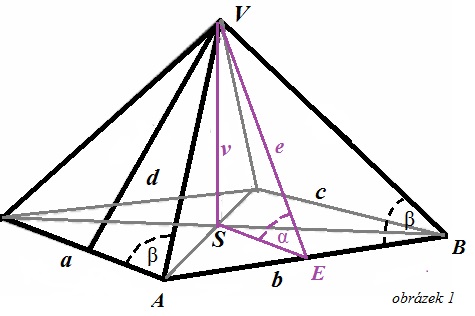
Úhel sklonu strany k základně α (alfa) je daný. Je to skutečný úhel sklonu strany Cheopsovy pyramidy, což je přesně 51°51’14”. Pro snadnější výpočet zaokrouhlíme na 52°. Úhel sklonu strany k základně α (alfa) a úhel strany β (beta) jsou dva rozdílné rozměry. Zjistíme si velikost úhlu β (beta) pro případné vytvoření formy na orgonity tvaru této pyramidy, a odhalíme při výpočtech různá matematická tajemství, která ve svých rozměrech Cheopsova pyramida skrývá:
Budeme počítat v centimetrech
Zadáme si pevnou délku základny b = 10 cm
Úhel sklonu strany k základně α = 51°51’14” = 52°
S těmito dvěma rozměry se dostaneme k mnoha informacím - hlavně matematickým, které jsou skryty v Cheopsově pyramidě.
A v pravoúhlém trojúhelníku úhel γ (gama) = 38° u vrcholu V
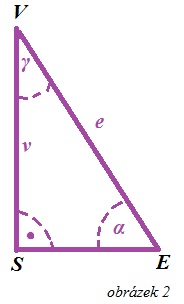
Potřebujeme zjistit výšku v, a délku přepony VE = e, tedy ve skutečnosti stranovou výšku pyramidy. Použijeme k tomu goniometrické funkce, kdy:
strana SE = ½ základny = 5 cm
úhel α = 52°
cos α = přilehlá / přepona
cos 52° = SE / VE (dále za použití matematických tabulek)
0,616 = 5 / VE
5 / 0,616 = VE
8,1168 = VE => známe rozměr strany VE,
podle Pythagorovy věty dopočítáme výšku pyramidy
VE na druhou = SE na druhou + SV na druhou
8,11682 = 5 na druhou + SV na druhou
65,8838 = 25 + SV na druhou
65,8838 - 25 = SV na druhou
40,8838 = SV na druhou
√40,8838 = SV
6,394 = SV => známe výšku pyramidy
Pro kontrolu můžeme udělat výpočet výšky přes funkci tg úhlu γ (gama). V pravoúhlém trojúhelníku je součet všech tří úhlů 180° . 180 - 90 - 52 = 38. Úhel je tedy 38°.
tg γ = protilehlá strana SE ku přilehlé (SV = v)
tg 38° = 5 / v
0,781 = 5 / v
5 / 0,781 = 6,40
výška pyramidy = 6,40. Výsledek souhlasí, drobná desetinná odchylka vzniká zaokrouhlením úhlu α = 51°51’14” = 52°
Z těchto vypočtených hodnot se můžeme pustit do výpočtu stranové výšky pyramidy.
Z obrázku 1 budeme počítat výšku strany VB trojúhelníku AVB, přičemž z minulých výpočtů známe rozměr e, který je nyní výškou trojúhelníku AVB, a délku základny. Abychom mohli využít vzorců pro výpočty pravoúhlého trojúhelníku, rozpůlíme si ∆ AVB na dva pravoúhlé, a použijeme k výpočtu ∆ VEB.
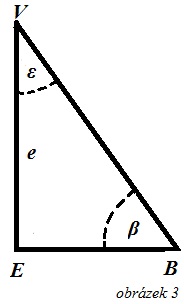
Potřebujeme zjistit délku přepony VB a úhel β, tedy ve skutečnosti výšku plochy strany pyramidy. Použijeme k tomu Pythagorovu větu a goniometrické funkce, kdy (z výpočtů na obr 2):
Výška VE = e = 8,1168
EB = ½ AB = 5
VB na druhou = VE na druhou + EB na druhou
VB na druhou = 8,11682 + 52
VB na druhou = 65,8824 + 25
VB na druhou = 90,8824
VB = √90,8824
VB = 9,5332
Hrana pyramidy VB na obr. 1 je 9,5332
úhel β = tg β = protilehlá ku přilehlé
tg β = VE / EB
tg β = 8,1168 / 5
tg β = 1,622
β = 58° 30’
Úhel strany pyramidy s délkou základny svírá - zaokrouhleno: 59°.
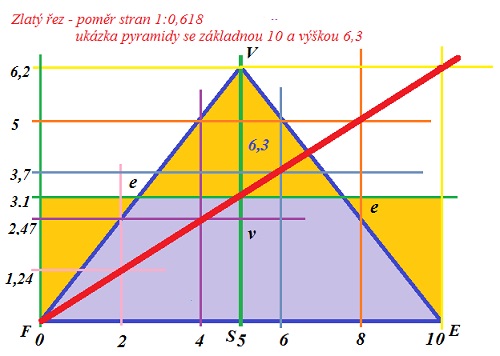
Podíváme se na "zlatý řez"

Poměr výšky pyramidy k délce základny odpovídá hodnotě "zlatého řezu", tedy poměru 0,618 : 1
(6,39 / 0,618 = 10; 10 / 1 = 10)
Zlatý řez je číslo φ (fí) = 1,618
Plocha středního řezu je délka základny násobená poloviční výškou pyramidy
Plocha základny = 10 * 10 = 100
Plocha středního řezu = 10 * 6,39 / 2 = 10 * 3,19 = 31,9

Podělíme-li plochu základny plochou středního řezu, dostaneme číslo π (pí) = 3,14
100 / 31,8 = 3,14
Říká se, že "zlatý řez" je znakem dokonalosti. J. Kepler řekl: "Geometrie má dva poklady: Pythagorovu větu a zlatý řez. První má cenu zlata, druhý připomíná spíše drahocenný kámen."
Podíváme se na číslo π (pí) zblízka
poměr obvodu základny pyramidy k dvojnásobné výšce pyramidy
4 x 10 / 2 x 6,35 = 40 / 12,7 = 3,14
je totožný s poměrem obvodu kružnice opsané k jejímu průměru
Průměr kružnice je stejný jako úhlopříčka základny pyramidy - zjistíme výpočtem dle Pythagorovy věty c2 = a2 + b2
d2 = a2
d2 = 102 + 102
d = √200
d = 14,1421
poloměr kružnice r
d / 2
14,1421 / 2 = 7,07
tedy zároveň
r = a / √2
7,07 = 10 / 1,4142
obvod kružnice
k = 2π x r
k = 2 x 3,14 x 7,07
k = 44,4
Poměr obvodu kruhu k jeho průměru:
44,4 / 14,14 = 3,14

Jelikož tedy délka obvodu základny pyramidy k dvojnásobku výšky je ve stejném poměru jako obvod kruhu k jeho průměru = 3,14 tedy Ludolfovo číslo π (pí) => vyplývá z toho, že v Egyptě bylo známo číslo π dlouho předtím, než bylo objeveno jinými kulturami, jak nám ukazuje naše současná historie.
Další fakt: V Cheopsově pyramidě je zakódována délka 185,7 metru (stranová výška), to připomíná řeckou míru "stadion". Vezmeme-li vzdálenost na zeměkouli mezi dvěma poledníky a podělíme ji 600, pak dostáváme 184,7. S rozměrem stranové výšky pyramidy jen půl procentní rozdíl. Platí-li tato teorie, pak délkovou míru převzali Řekové od Egypťanů a Egypťané věděli, už dávno před Koperníkem, že Země je kulatá!
Více o číslu pí a fí se dočtete na tomto odkazu níže: http://www.zlate-mince.cz/CRM_Konstanty_Pi_Fi_Au.htm#
Přepočet rozměrů pyramidy na naši nadmořskou výšku
Tyto pyramidy mají v naší oblasti větší energetický dosah, avšak nesouhlasí žádné matematické vzorce a propočty, jako u Cheopsovy pyramidy. Energetické vyzařování je slabší, než u Cheopsovy pyramidy, ale obsáhne větší plochu.
Cheopsova pyramida obsáhne svým působením plochu menší, avšak její energetické vyzařování je silné.
Úhel stranové výšky je 65°, a stejným propočtem, jako u Cheopsovy pyramidy získáme úhel pro výrobu formy, tedy úhel strany k základně. Výpočtem dosáhneme výsledku 67°.
=========
"Teorie vyzařování energie říká, že energie vyzařovaná pyramidou se soustřeďuje ve všech pěti vrcholech pyramidy, čímž vytváří paprsky, které se znovu spojují ve fokálním bodě, zvaném královská komora, nacházejícím se v jedné třetině mezi základnou a vrcholem. Největší účinky má pyramida jejíž stěny svírají s podstavou úhel 51°51´ a je-li orientována stěnami na světové strany."
=========
